A Ritchey–Chrétien telescope (RCT or simply RC) is a specialized variant of the Cassegrain telescope that has a hyperbolic primary mirror and a hyperbolic secondary mirror designed to eliminate off-axis optical errors (coma). The RCT has a wider field of view free of optical errors compared to a more traditional reflecting telescope configuration. RCts are wide-spread in professional and high-end observatories and space telescopes like Hubble Space Telescope (HST) or the 10.4 m Gran Telescopio Canarias at Roque de los Muchachos Observatory on La Palma, Canary Islands, (Spain).

Advantage:

• wider field of view
• short tube length
• very good  coma elimination

Disadvantage:

• severe large angle astigmatism
• quite difficult collimation (see section about Collimation)

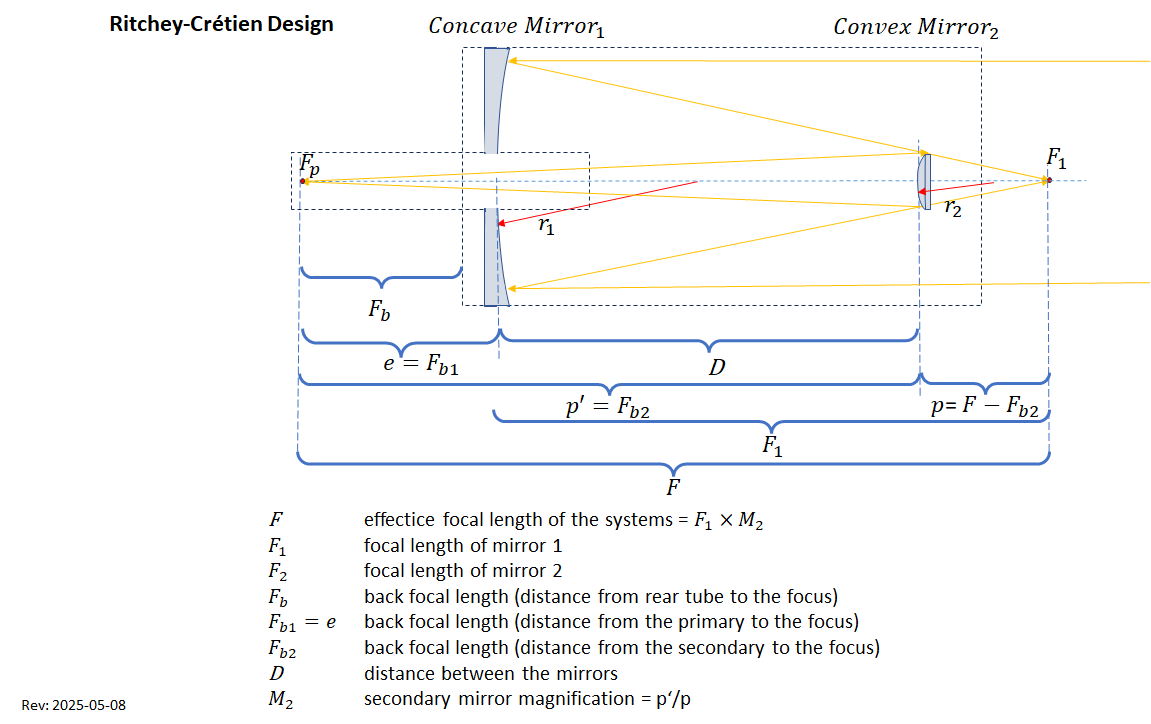
Relationship between mirror distance and focal length

Especially in RC telescopes with their hyperbolic mirrors, there is a non-linear dependency between the focal length and the distance between the two mirrors, but this dependency or mirror distance factor is not disclosed by the manufacturer. 

From the equations below it can be deduced that the focal length (and thus the backfocus) of the system is inversely proportional to the mirror distance:

• The smaller the mirror distance, the greater the focal length or backfocus, and vice versa.

Corrective action

• If the measured focal length or backfocus is less than nominal, the mirror distance is too large:
• In this case, the collimation screws X, Y, Z must be turned clockwise to reduce the mirror distance.
• - If the measured focal length or back focus is greater than the nominal value, the mirror distance is too short:
• In this case, the collimation screws X, Y, Z must be turned counterclockwise to increase the mirror distance.

Example:

Supposedly the Distance Factor (Delta D / Delta F) for the TS1624rASI294  telescope is said to be 1:6, i.e. to increase the focal length or backfocus by 1mm, the mirror distance must be reduced by 0.1667 mm.

WARNING: The distance factor of 6 has been found somewhere on the Internet and has not yet been confirmed.

In the previous example with a measured focal length error of -8.74 mm (too short), the mirror distance must be reduced by:

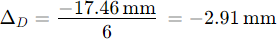
Some more formulas:

Primary and secondary mirror radius:

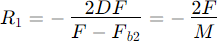
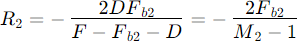
Secondary mirror magnification

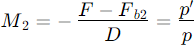
Backfocus behind the primary mirror (if D and 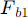are known)

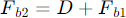
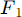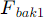Mirror distance (if and are known):[1]

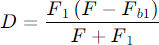
Simplified equation for the focal length of RC telescopes  

in relation to mirror distance and mirror focal lengths:

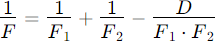
solved for focal length:

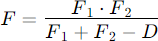
solved for mirror distance D:

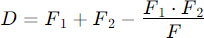
Mirror distance equation [2]

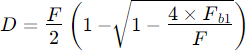
However, it's important to note that the actual relationship is more complex due to factors such as mirror curvatures, aberrations, and other optical properties. For precise calculations, optical design software or specific telescope design equations are typically used.

Since F1 and F2 are constants in a given telescope, the correct distance between the two mirrors at the end is a non-linear function D = f(F), which resolves to F = f(D) and can roughly be expressed by a factor: the Distance Factor.

Focal length equation for primary mirror [2] 

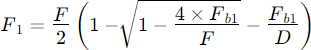
Focal Length equation for secondary mirror [2] 

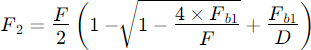
However, it's important to note that the actual relationship is more complex due to factors such as mirror curvatures, aberrations, and other optical properties. For precise calculations, optical design software or specific telescope design equations are typically used.

Since F1 and F2 are constants in a given telescope, the correct distance between the two mirrors at the end is a non-linear function D = f(F) but can roughly be expressed by a factor: the Distance Factor

Credit: 

[1] Wikipedia

[2] ChatGPT

Created with the Personal Edition of HelpNDoc: Easily create PDF Help documents